Quanto é 0 elevado a 0?

Não é uma pergunta sem resposta, é uma pergunta difícil de responder mas que as pessoas que a sabem responder pensam ter a certeza que estão certas, mas não estão (segundo outras).
A mim, pessoalmente, foi-me ensinado que qualquer número elevado a 0 é igual a 1!
Mas isto é a minha opinião, vamos perguntar ao pessoal dos números...

Reparem no que aconteceu quando eu perguntei "Quanto é ?" a um grupo de gente com cabeça:

---

Estudante inteligente:
E.I.: Já sei!
E.I.: =   = = = .E.I.: Agora substituindo o x por 0 vemos que =1

---

Estudante ainda mais inteligente:
E.A.M.I.: Assim está errado, não podes dividir por 0 como fizeste no último passo, portanto a resposta é:
E.A.M.I.:  =  =  = = 
E.A.M.I.: Substituindo o x por 0, e visto que 0x0 é 0, chegamos à conclusão que = !

---

O estudante mais inteligente de todos:
E.M.I.T.: Assim também não funciona, porque se  então  é igual a  
E.M.I.T.: Por isso no teu terceiro passo também fazes a divisão por zero, errado!
E.M.I.T.: Em vez disso podemos olhar para a função  e ver o que acontece quando x>0 fica mais pequeno. Assim temos:

=

=

=

=

=

=

=

=

= 1

E.M.I.T.: Então, como   = 1, isso significa que = 1.

---

Professor Universitário:

P.U.: Mostrar que 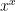 se aproxima de 1 como um valor positivo a descair para o 0, não prova que .

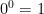P.U.: O facto de a variável x ter um valor próximo de zero é diferente de ser exactamente 0.

P.U.: Desta forma prova que  é um valor indefinido, não tem valor!

---

Professor de Cálculo Avançado:

P.C.A.: Para todo o , temos

P.C.A.: Logo,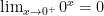

P.C.A.: Isto é quando o x se aproxima de 0 (mas continua positivo),   fica .

P.C.A.: Por outro lado, para número reais y se 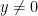, temos

P.C.A.: Logo , quando o y se aproxima de 0,  fica 1.  

P.C.A.: Então, vemos que a função  tem descontinuidade no ponto (0,0).

P.C.A.: Em particular, quando nos aproximamos desse ponto pelo eixo das ordenadas, temos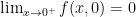

P.C.A.: Mas se aproximarmos desse ponto pelo eixo positivo das abcissas, temos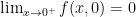

P.C.A.: Quero dizer com isto que o valor de  vai depender da direcção que tomamos o limite. Isto significa que não há forma de definir  de forma a que a função  seja contínua no ponto (0,0).

---

Matemático:
M.: Zero elevado a zero é 1. Porquê? Porque nós dizemos que sim! Não, é porque é mesmo verdade.
M.: Vamos considerar o problema em definir a função  para inteiros positivos x e y.
M.: Há tantas definições que nos dão resultados idênticos, por exemplo, uma idéia é usar para nossa definição o seguinte:
M.: =  - onde o y é repetido x vezes. Nesse caso se o x for 1, temos = .
M.: Esta definição extende-se desde os negativos inteiros até aos positivos. Logo se y for 0, temos
M.: Vês, já provei que ! Mas isto é só uma possível definição para .


M.: Podemos tentar outra. Por exemplo, supõe que decidimos definir  com esta expressão:  :=
M.: Por palavras, significa que o valor de  é definido pelo , número real z que se aproxima ficando mais e mais pequeno aproximando-se do valor x. [Working with z>0]
M.: Interessante, usando esta definição, podemos ter = = =
M.: Então, vamos ver que  e não 1.


M.: Garantidamente, esta definição que fizemos agora parece estranha mas vai de acordo ao senso comum do que  significa para todos os números reais positivos de x e y e desta forma a função tem continuidade à medida que nos aproximamos de x=0 e y=0
M.: Então qual destas 2 definições está certa? O que é o  afinal? Bem para x>0 e y>0, já sabemos o que queremos dizer por . Mas quando x=0 e y=0, a fórmula não tem significado óbvio.
M.: O valor de  vai depender da nossa escolha de definição do que é que entendemos por essa afirmação. [WTF]
M.: A nossa intuição sobre o valor de  para valores positivos de y e x não é suficiente para concluir o valor de  para valores nulos.


Eu.: Então se é assim, porque é que os matemáticos dizem com todas as certezas que ?
M.: Bem, acho que é porque dá mais jeito. Algumas fórmulas mais "importantes" ficam menos agradáveis se em vez de 1, nós usássemos o , ou se disséssemos que era indefinido.


M.:Por exemplo veja o Teorema Binomial que diz o seguinte:
M.:  =  - onde  são os coeficientes binomiais.
M.: Desta forma se colocarmos o a=0, assumindo que  temos:
 =  =
=
=
=
M.: Onde digo que  para todo o k>0, e . Agora acontece que já temos o factor mágico .
M.: Por isso, se  não fosse igual a 1, então o teorema binomial não funciona quando o a=0 porque o  já não é igual a
M.: Se nós usássemos o , ou disséssemos que o valor é indefinido, o teorema estava certo apenas até certo ponto, exceptuando o caso de cima.


M.: Há mais razões pela qual usamos o valor 1, mas chegamos sempre à mesma conclusão se as explicasse - É preferível o 1 aos outros resultados todos, para alguns teoremas baterem sempre certo, assim é mais natural e correcto para a matemática.
O resultado não é o mais correcto, é o certo!


- Deixo a pergunta, como é que ainda há gente que não gosta de matemática...